III) Üçgen Eşitsizliği

Bir üçgende iki kenar uzunluğu toplamı, üçüncü kenar uzunluğundan büyüktür.

➞ a < b + c

➞ b < a + c

➞ c < a + b 

şeklinde yazabiliriz.

Yine benzer bir mantıkla, üçgenin bir kenar uzunluğu diğer iki kenar uzunluğundan küçük; farklarının mutlak değerinden büyüktür. Aksi halde çok uzun olan bir kenar için diğer iki kenar birleşemez ve üçgen oluşturamaz. Üçgenlerdeki bu bağıntıya üçgen eşitsizliği denir. 

➞ b - c < a < b + c 

➞ a - c < b < a + c

➞  a - b < c < a + b

 II) Üçgende Açı Kenar Bağıntıları

Bir üçgende kenar uzunlukları karşısında bulunan açının ölçüsüyle doğru orantılıdır. Bir açı ne kadar büyükse karşısındaki kenar o kadar büyük, bir açı ne kadar küçükse karşısındaki kenar o kadar küçük olur. 
Örnek olarak bize m(C) > m(B) > m(A) bilgisi verilirse bundan yola çıkarak c > b > a yorumunu yapabiliriz.

Ayrıca bir açının büyüklüğüne göre kenarlar arasında bağıntı kurabiliriz.

alfa < 90° ise b^2<a^2+c^2

alfa=90° ise  b^2=a^2+c^2

alfa>90° ise b^2>a^2+c^2

 ÜÇGEN NEDİR?

Aynı doğrultuda bulunmayan 3 noktanın birleştirilmesiyle oluşan geometrik şekle üçgen denir. Her üçgenin kenarları arasında üçgen eşitsizliğine uyan bir bağıntı bulunur. Bu bölümde üçgenleri, açıları ve kenarları arasındaki ilişki yönünden inceleyeceğiz. 

I) Üçgende Açılar

Üçgenin iç açıları toplamı 180 derecedir ve toplamda 3 açısı bulunmaktadır. Bu açılar arasında aşağıdaki açı özelliklerine göre isimlendirilir.

1) Üçgende Açı Özellikleri  

Dar Açı: Büyüklüğü 0 ile 90 derece arasında olan açılardır.

Dik Açı: Büyüklüğü 90 derece olan açıdır.

Geniş Açı: Büyüklüğü 90 ile 180 derece arasında olan açılardır.  

Doğru Açı: Büyüklüğü 180 derece olan açıdır.

Tam Açı: Büyüklüğü 360 derece olan açıdır.

Tümler Açı: Toplamları 90 derece olan açılardır.

Bütünler Açı: Toplamları 180 derece olan açılardır.

Açıortay: Bir açıyı iki eş açıya ayıran ışına açıortay denir.

2)Üçgenin Açıları

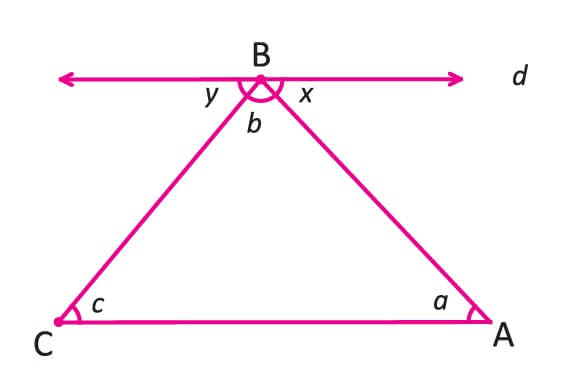
Bir üçgenin iç açıları toplamı 180 derecedir.Bunun kanıtını üst taraftaki görselde görebiliriz. Bir ABC üçgeninin B noktasından geçen ve CA kenarına paralel bir doğru çizdiğimiz zaman Z kuralından a açısı x açısına, c açısı da y açısına eşit olacaktır. b, x, y açıları bir doğru açıyı oluşturduklarından toplamları 180 derece olacaktır. Buradan üçgenin iç açıları olan a, b, c açılarının toplamı da 180 derece diyebiliriz.

x+b+y = 180

a+b+c = 180 

 

3) Üçgende Açıortay Özellikleri

Bir üçgende iç açıortaylar bir noktada kesişir. Bu nokta, üçgenin iç teğet çemberinin merkezidir. Aşağıda vereceğim açıortay özellikleri aslında birkaç işlem sonucu kendinizin de bulabileceği sonucu direkt ezberleyip soruları hızlıca çözmeniz için verilmiştir. Bu işlemleri aklınıza oturması için anlatacağım.

Bir üçgende iki açıortay arasındaki açının ölçüsü. açıortayı çizilmeyen açı ölçüsünün yarısından 90 derece fazladır. ABC üçgenine baktığımızda A açısının ölçüsünü 180 dereceden çıkarttığımızda iki açıortayın toplamını yani 2x+2y elde ederiz. Bulduğumuz bu sonucu ikiye böldüğümüzde ise açıortayların birer tanesinin toplamını x+y buluruz. Şimdi BCD üçgenine baktığımızda artık iki açının toplamını biliyoruz ve bunu 180 dereceden çıkardığımız zaman bize a açısının değerini verecektir.

m(A) + 2x + 2y = 180 

2x + 2y = 180° – m(A)

x + y = {180° – m(A)} / 2

a + x + y = 180° 

a = 180° – (x + y) 

a = 180°– {{ 180 – m(A)} / 2} 

SONUÇ: a = 90° + {{m(A)} / 2}

  

Bir üçgende iki dış açıortay arasındaki açının ölçüsü ile açıortayı çizilmeyen iç açının ölçüsünün yarısı, birbirinin tümleridir. Burada da temel mantığı anlamamız için işlemleri kısaca anlatacağım fakat göstermeyeceğim. BCD üçgenine baktığımızda 180 dereceden açısını çıkardığımızda x+y değerini  a değeri cinsinden buluruz. ABC üçgeninin dış açıları olan 2x ve 2y açılarını 180 dereceden çıkardığımız zaman iki iç açısını buluruz. bu iç açıları da 180 dereceden çıkardığımız zaman m(A) açısına ulaşırız. Bulduğumuz değerde x+y gördüğümüz yere 180-a yazdığımız zaman aşağıdaki sonuca ulaşırız.

a + {{m(A)} / 2 = 90   veya    a = 90 - {{m(A)} / 2 }   

Bir üçgende bir köşenin iç açıortayı ile diğer bir köşenin dış açıortayı arasındaki açının ölçüsü, açıortayı çizilmeyen köşenin iç açı ölçüsünün yarısıdır.

  a = {{m(A)}/2} veya  2a = m(A) 

Bir üçgende farklı köşelerdeki iki dış açıortay ile bir iç açıortay bir noktada kesişir.

4) İkizkenar Üçgen 

İki kenarının uzunluğu eşit olan üçgenlere ikizkenar üçgen denir.

➞ ABC üçgeninde [BC] taban, [AB] ve [AC] yan kenarlardır.

➞ A tepe açısı, B ve C taban açılarıdır.

➞ |AB| = |AC|

➞ m(B) = m(C)

➞ İkizkenar üçgende tabana ait yükseklik, hem açıortay hemde kenarortaydır.

5) Eşkenar Üçgen

➞ Üç kenarının uzunluğu eşit olan üçgenlere eşkenar üçgen denir.

➞ |AB| = |AC| = |BC|

➞ m(A) = m(B) = m(C)

➞ Eşkenar üçgen ikizkenar üçgenin özelliklerini sağlar.

  

ÜÇGENLERDE TEMEL KAVRAMLAR

     

➟ÜÇGEN NEDİR? 

➟ÜÇGENDE AÇILAR

➟ÜÇGENDE AÇI ÖZELLİKLERİ

➟ÜÇGENİN AÇILARI

➟ÜÇGENDE AÇIORTAY ÖZELLİKLERİ

➟EŞKENAR ÜÇGEN

➟İKİZKENAR ÜÇGEN

➟ÜÇGENDE AÇI KENAR BAĞINTILARI

➟ÜÇGEN EŞİTSİZLİĞİ